熱力学の教科書では、カルノーサイクルという熱機関モデルを使い熱移動で仕事エネルギを外部に取り出す説明をする。しかし、何が分からないのかもわからない説明だった。モデルが伝えたいことが何かわからかった。
今なら言える。可逆的に熱移動をさせてエネルギーを取り出すことを表現しているのがカルノー熱機関だと。数式も何回も読むと記憶されて、自然に何か分かった気分になる。時間がたつとまたすっきりしなかった。可逆の概念にたどり着いてなかったから。
前回の説明で最後に登場させたエントロピーという言葉と可逆的な熱移動を結びつけた。しかし、まだすっきりしないはずだ。もう少し直感的にエントロピーのイメージを説明したい。
熱エネルギーを温度とエントロピーの積で表現する。この表現は熱力学の根底にある。簡単な式なので記憶しやすいから、理解した気分にさせる。
中学校の理科でも、熱エネルギーは熱容量と温度変化の積で表現した。熱エネルギーが温度とエントロピーの積で表現するのと式の形は同じで相通じる。
中学校では熱容量が一定で温度が変化する場合を扱っていた。熱力学では、熱を担うもの(量や状態の数)が変化する成分がさらに加わる。熱を担うものが熱容量でなくエントロピーという言葉に変わっている。
温度が一定、圧力一定で風船を可逆的に膨らませる。体積を大きくすると、内部エネルギーが増加する。これを描くと温度を一定にしたままエントロピーの増加のイメージができる。
付録3はエントロピーの直感的理解を助けてくれる。
コラムColumn
質の違うものの接触がエネルギーを放出するという真実(5)
Vol.13-18
2025年08月07日
質の違うものの接触がエネルギーを放出するという真実(5)
この記事の内容
質の違うものの接触がエネルギーを放出するという真実(5)
付録3 熱エネルギーQを温度TとエントロピーSの変化量で表現することの説明
熱エネルギーQを温度Tとエントロピー変化δSの積で表現できることを仮定した。これが基本的であるのだが、説明しなくてもそうだと思う人もいるだろう。高校で以下の理想気体の状態方程式を学んだ。
PV=nRT (Rは気体常数、nはモル数、Pは圧力、Vは体積)
この式の左辺も、右辺も気体のエネルギーに相当する(厳密には3/2nRTが内部エネルギー(熱エネルギー)というが、ここでは3/2は無視する)。
仮定した熱エネルギーQ=TδSと状態方程式と見比べるとδSはnRに相当している。δSが増加するのはn(気体の量または分子の数)が増加するのに相当する。
圧力一定なら体積が増加することに相当する。その概念を図2-3に示す。
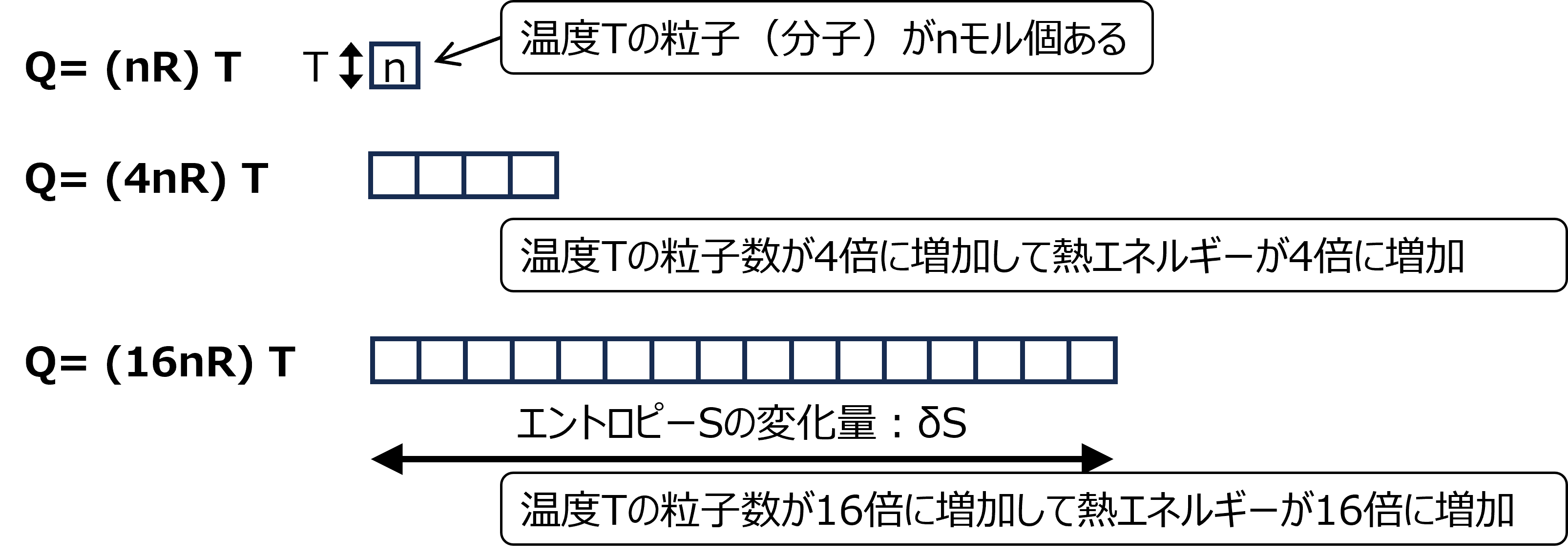
図2-3 エントロピー変化δSの疑念図
( )の中がエントロピー変化量δSに相当する。Qは熱エネルギー。
[ Author : Y. F. ]

