図2-6にキャパシタ1,2が並列接続されて合体したキャパシタを示す。
2つのキャパシタが持っていた電荷の合計4Qは2等分されて保存される。同じ電荷2Qが蓄積されたキャパシタが並列接続された状態て混合(合体)は終わる。
同じ電荷2Qを蓄えた2つのキャパシタの持つエネルギーE12は:
E12=1/2・ 2C (V12)2 = 1/2・2C (4Q/2C)2
=8/2・ Q2/C
ここで
2C:並列接続されたキャパシタ2つのキャパシタンス
V12: 並列接続されたキャパシタに電荷4Qが蓄えられているときの発生電圧
と計算される。
2つのキャパシタが離れて孤立していたときのエネルギーE1+E2を思い出すと、
E1+E2=10/2・Q2/C
だった。
E12とE+E2を比較してみると、エネルギーE12は、孤立していたときのエネルギー(E1+E2)よりQ2/Cだけ小さい。即ち、結合するとエネルギーは失われていることになる。
結合されて一体になると、電荷は保存されているのに孤立して離れていた時よりもエネルギーの一部を失っている。
結合することが、どのようにして、エネルギーを失わさせるのか、計算をしてみよう。
質の違うものの接触がエネルギーを放出するという真実(7)
Vol.13-18
2025年10月21日
質の違うものの接触がエネルギーを放出するという真実(7)
この記事の内容
質の違うものの接触がエネルギーを放出するという真実(7)
異質なものを接触させるという真実とその表現の例3
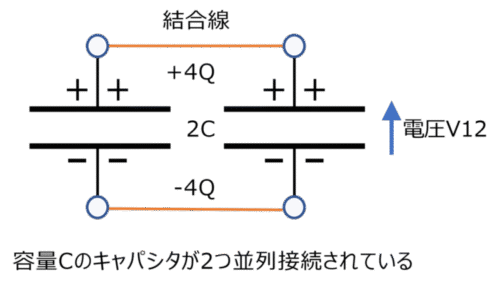
図2-6 電荷量2Qが容量Cのキャパシタ1,2に蓄えられて、並列接続されているキャパシタの図
失われたエネルギーを計算してみる。2つのキャパシタを結合させて図2-6のキャパシタにする。
結合方法はいろいろある。一つの方法として有限の抵抗値の抵抗を介して電荷を移動させて結合させる。それを図2-7に表した。
電荷が移動するとき電流が流れる。そのときの抵抗に流れる電流Jを計算する。電荷が時間をかけて移動して混ざり、電荷が等分されるまで移動する。
専門的な計算になるので、ここはスキップしても構わない。以下に抵抗Rを通して電荷が移動するときの電流Jをまず計算する。
J=(V1-V2)/R
ここで
V1-V2:キャパシタC1とC2の電位差
微小な時間dtの間に微小な電荷量dQがキャパシタC1からC2に移動して電位差V1-V2に微小な変化 d(V1-V2) と微小な電流変化dJが生じる。この関係を表現すると
dV1=-dQ/C dV2=dQ/C
移動した微小な電荷量は電流Jと微小時間dtの積であるから
dQ=Jdt
電流Jの微小な変化dJを時間微分dtを用いて表現すると
dJ=(dV1-dV2)/R=-2dQ/RC=-2Jdt/RC
表現の変形を続けると
dJ/dt=J’=-2J/RC
J’/J=-2/RC
㏑J=-2t/RC+定数
J=exp(-2t/RC+定数)
t=0の時 J=(3Q-Q)/RC=2Q/RCなので定数がきまり、電流の表現が得られる。
J=2Q/Rcexp(-2t/RC)
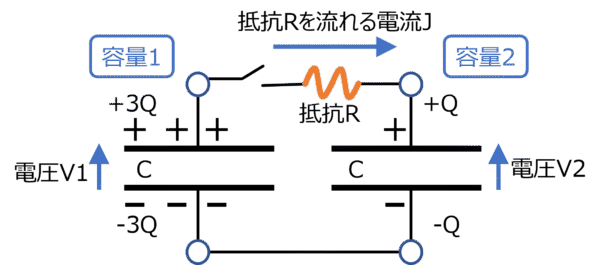
図2-7 抵抗Rを通して電荷が容量1から容量2に流れることを示す図
[ Author : Y. F. ]

