次に2つのキャパシタが結合して失う発熱エネルギーの計算をする。ここも専門的なので、スキップしても構わない。
電気がキャパシタ1から2に移動するとき、抵抗Rは発熱する。これを図2-8に示す。
発熱エネルギーを時間積算して全発熱量Lを計算する。
W=R*J2=4Q2/RC2exp-4t/RC
ここで
W:瞬間の発熱量
均一に電荷が分布するまで発熱は続く。発熱量Lを時間関数で見積もる。Wを時間積分して
L=∫Wdt=(-RC/4)4Q2/RC2exp(-4t/RC)+定数
= -Q2/Cexp-4t/RC+定数
t=0 のときL=0 なので定数=Q2/Cとわかる。よって
L(t)=Q2/C(1-exp(-4t/RC))
時間が無限に経た全発熱エネルギーはt=∞にして得られ、Q2/Cである。これは混ざったことで失った損失エネルギーの値である。
キャパシタC1,2が独立して離れてあるときのエネルギーE1+E2と結合が終わったときのエネルギーE12の差と全発熱量L(t=∞)は一致した。
質の違うものの接触がエネルギーを放出するという真実(8)
Vol.13-18
2025年10月21日
質の違うものの接触がエネルギーを放出するという真実(8)
この記事の内容
質の違うものの接触がエネルギーを放出するという真実(8)
異質なものを接触させるという真実とその表現の例4
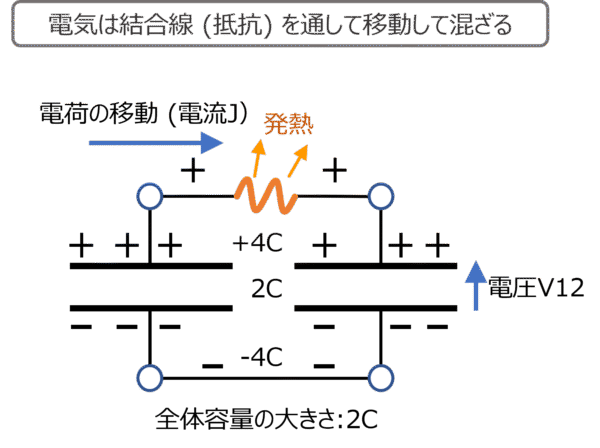
図2-8 抵抗Rを通して電流が流れて発熱するときの回路図
電荷の量が違うキャパシタを結合した時に放出するネルギーを計算した。電荷の量が違うと電圧という質の違いが生まれる。電圧が違うと、電荷は電圧の高いほうから、低いほうに移動する。
移動するとき、移動のための道が導線ならその抵抗値に見合った発熱をしながらエネルギーを放出する。抵抗が大きいと電荷は移動しにくいので、長い時間をかけて移動する。抵抗が小さいと、瞬間に大電流が流れる。
ここでは蓄積された電荷の量が異なるキャパシタの結合(電荷の移動)を例に取り上げた。
電荷の移動の表現は、温度の違う水の混合とよく似ている。電荷Qを熱エネルギーQと読み替え、電圧Vを温度Tと読み替えても同じ表現が得られる。
高温T1の水と低温T2の水を混合させるとき、高温から低温に向かって熱が流れる。混合によりもともと持っていた全熱エネルギーQは保存されないで失われた。
これを思い出すために熱エネルギーのことを再表現してみる。
Q1=CT1 Q2=CT2
ここで
C:熱容量
Q1+Q2:孤立していた水の持っていたエネルギー
高温と低温を混ぜたあとの熱エネルギーQ12は
Q12=Q1+Q2-L
ここで
L:混合により失うエネルギー
電気の話も水の話もよく似ていることが分かると思う。ここでもう一つ分かることがある。
混合により失うエネルギーの表現
Q12=Q1+Q2-L
を変形して
Q12+L=Q1+Q2
としてみよう。
元から見るとLは損失として見えるが、混合により得られるエネルギーとみることができる。即ち異質なものが接触して混合すると、エネルギーを生み出すことを表現している。
そのエネルギーを利用すれば何かできる。
社会現象も類似している。貧富という質の差は孤立していると分からないが、接触すると、差が分かる。その差はエネルギー(意欲や暴動、金銭欲など)として表れる。
国の活力の差も一人一人の活力が積算されて、例えば人口やGDPというものに表現されて、社会現象として表れていると思う。
思考実験をするとこのことが良く理解できる。日本の人口は1.3億人だがこの人口が減り続け、 GDPは30年間も一定のままだ。
仮に一人一人が同質の人だとしたら、 GDPは増えるだろうか。仮に一人一人が同じくらいの暮らしぶりならGDPは増えるだろうか、減るだろうか。仮に一人一人が幸せならGDPは増えるだろうか。
答えは明らかでありGDPは減少するだろう。
異質な人が社会を構成したらどうだろうか。平等でない社会が生まれ、富裕層も生まれるが貧民層も生まれる。羨望や意欲が生まれるが、犯罪もおきるだろう。
同質の人の接触ではエネルギーが生まれないだろう。
社会現象の予測はこのコラムで説明した水や電気の接触で理解できるように思える。
[ Author : Y. F. ]

