Truth that Contacting of Different Qualities Releases Energy (3)

Next, let us consider a method of transferring heat from water 1 to water 2 using a reversible heat engine that moves heat in a reversible manner. By doing so, we will arrive at a different answer. Now, let us describe the process of transferring heat slowly and quietly in a reversible way.
The concept of "reversibility" will be expressed using the thermodynamic term "entropy." It is not necessary to fully understand the concept of entropy at this stage, but since it will appear again later, this will be a good opportunity to become familiar with it.

When energy is transferred in a reversible manner, there is no change in entropy. To help you intuitively understand the concept of entropy, I have prepared Appendix 2.

Now, let’s calculate the entropy changes for water 1 and water 2. We will denote the entropy change of water 1 as δS1 and that of water 2 as δS2. Assuming the final temperature Tm after water mixing is unknown, we will integrate the infinitesimal changes in entropy as heat is transferred until the temperature reaches Tm.
From Appendix, since the infinitesimal change is given by dS = dQ / T, the following expressions can be written.

Similarly, the following expressions can be written for Water 2.

Tm is the assumed temperature after mixing.

Heat energy is transferred from Water 1 to Water 2 till both temperatures reach to Tm by using a reversible heat engine. Afterward, by combining (mixing) Water 1 and Water 2 at the same temperature Tm, a mixed body of water at temperature Tm is obtained.

The condition of reversibility is expressed by the total entropy change being zero (see Appendix 2.). The total entropy change is represented by the sum of δS1 and δS2.
Therefore, the total entropy change is given as follows.

Since "transferring heat through a reversible process" is expressed as "total entropy change δS = 0," it can be represented as follows.

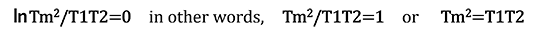
Furthermore, modifying the expression it gives:

If T1 = 80℃ and T2＝40℃, then the following calculation can be performed.

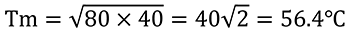
This temperature is lower than the 60℃ answer given by elementary school students. The decrease in temperature shows that working has been done on the outside with energy loosing. By storing the work energy that is released and returning it to the water, the temperature will reach 60℃.
If work energy is released to the outside while mixing, it becomes a loss energy that cannot be recovered. It is also equivalent to saying that mixing cannot occur without energy release.
If work energy is released and dissipated, it cannot return to its original state without external energy assistance.

[ Author : Y. F. ]