The calculation of how much energy can be released is possible. Since the mixing temperature without loss is calculated to be 56℃, the calculation of loss is straightforward.
The sum of the original energies of water 1 at 80℃ with heat capacity Ct and water 2 at 40℃ with the same heat capacity (E12), and the difference between the energy of the mixed water at 56℃ with heat capacity 2Ct (Em), gives the energy that can be released (W).
E12 = 80Ct + 40Ct (The thermal energy that water 1 and 2 had before mixing)
Em = 56×2Ct (The thermal energy after mixing reversibly)
W = E12 – Em = (80 + 40 - 2 × 56) Ct = 8Ct (The maximum energy that can be released)
Here, I just wanted to explain the basic idea, so I avoided using technical terms like absolute temperature and specific heat capacity at constant pressure.
In conclusion, I explained the truth that "the contact of different substances releases energy" using the example of the contact between hot and cold water.
The explanation was simplified to make it intuitively understandable. Examples of different temperature substances touching and mixing, which release energy, are abundant in our everyday environment.
1) Rain or snow, winds, and the resulting storms and disasters caused by the contact between moist warm air and dry cold air.
2) A tornado in which warm air spirals upwards toward cold air in the sky.
3) Lightning caused by the charges carried by upward air currents moving toward cold air.
4) Ocean currents and convection created by the interaction of cold and warm currents.
A large temperature difference results in a correspondingly large release of energy. The difference in quality is not limited to temperature alone. Differences in people's temperament, passion, and cultural education lead to disparities in national power, GDP, population, marriage, patents, and other factors, which are expressed in various forms. I believe this can be explained in this column, "Social Phenomena Overlaying Thermodynamics."
Truth that Contacting of Different Qualities Releases Energy (4)
Vol.13-18
May 9, 2025
Content of This Article
Truth that Contacting of Different Qualities Releases Energy (4)
Appendix 2: An intuitive explanation of the truth of "reversible heat transfer" expressed as "change in entropy = 0."
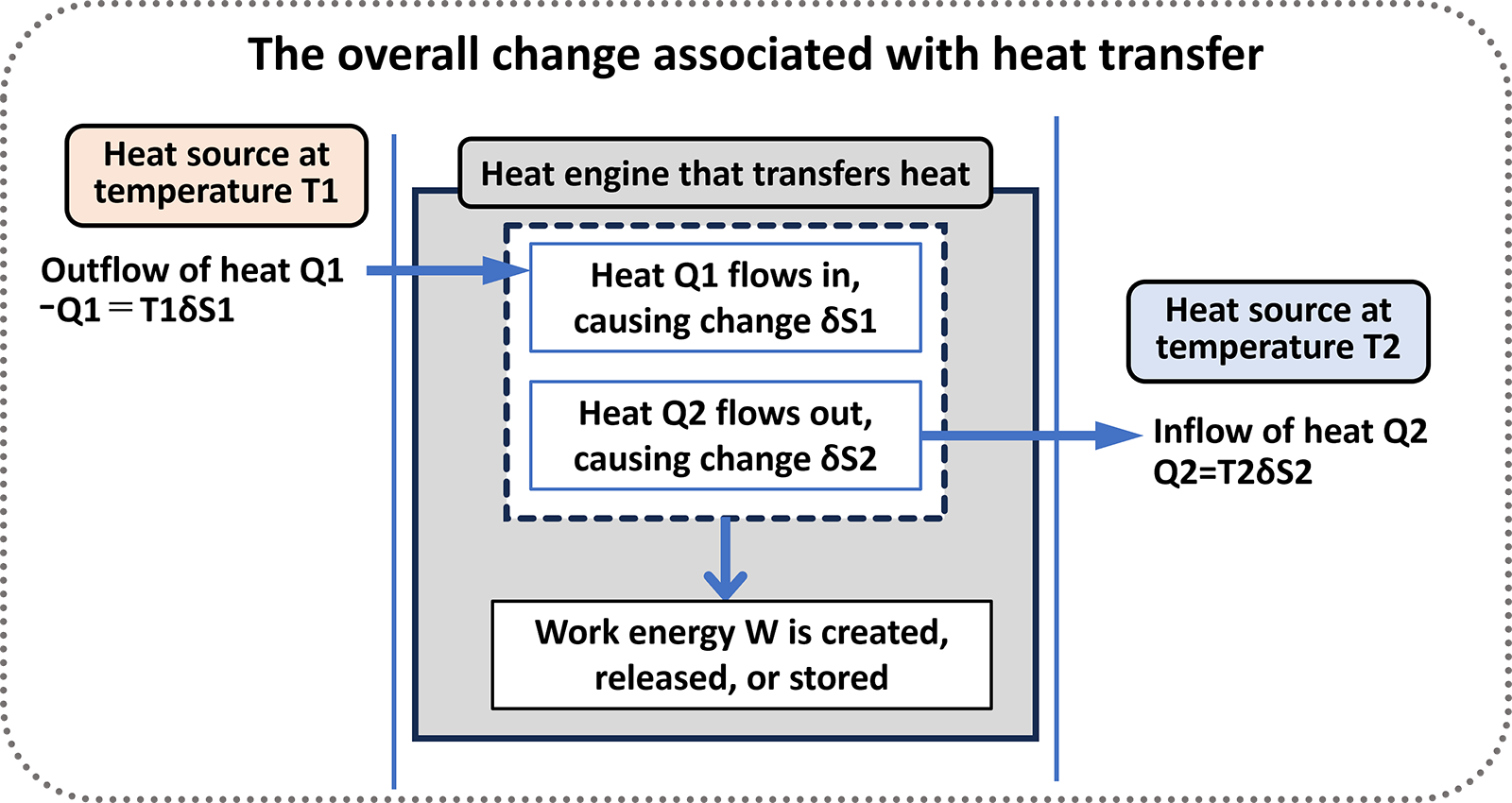
Figure 2-2: A conceptual diagram of operation of heat engine transferring heat from a high-temperature heat source T1 to a low-temperature heat source T2.
Heat energy Q1 flows out from the high-temperature heat source and enters the heat engine, creating change δS1. Heat energy Q2 flows from the heat engine to the low-temperature heat source, creating change δS2. At this time, work energy W is either released or stored.
In Figure 2-2, operation of heat engine transferring heat energy is conceptually shown. Heat Q1 flows in, and heat Q2 flows out. The heat engine generates work energy W, which is the difference between Q1 and Q2. The influx (increase) of energy is represented with a positive sign, and the outflow (decrease) is represented with a negative sign. To express the conservation of energy, the following equation holds.
Q1=W+Q2 or Q1-Q2=W
Assuming that the transferred heat energy Q creates changes in the heat engine and heat source, resulting in a change δS, this can be expressed in terms of temperature T and the change δS as follows:
Q=TδS
This expression may feel somewhat intrusive. In Appendix 3, which will be published next time, an illustration of this linear expression will be convincingly provided.
Changes in the heat engine caused by heat transfer are expressed using change in δS as follows:
Q1=T1δS1 (Heat Q1 moves reversibly from the heat source to the heat engine.)
-Q2=T2δS2 (Heat Q2 moves reversibly from the heat engine to the heat source.)
After heat transfer is completed, if change in the heat engine is zero and it returns to its original state, the engine can be operated in reverse. That is, by reversing the operation of the heat engine, heat Q2 can flow in from the low-temperature heat source, work energy W can be inverted into heat, and the original energy Q1 can be returned to the high-temperature heat source.
Total change δS = 0 in the heat engine expresses the reversible operation of heat transfer.
Therefore, following expression is obtained.
δS1+δS2=0 or Q1/T1 -Q2/T2=0
Up to this point, the term "change" referred to as δS is called entropy change.
[ Author : Y. F. ]

