Figure 2-6 shows the capacitor formed when capacitors 1 and 2 are connected in parallel and combined. The total charge 4Q, which the two capacitors originally held, is divided equally and preserved. The process of mixing (combination) ends when two capacitors, each storing the same charge 2Q, are connected in parallel.
The total energy E12 stored in the two capacitors, each holding the same charge 2Q, is:
E12=1/2・ 2C (V12)2 = 1/2・2C (4Q/2C)2
=8/2・ Q2/C
here
2C: capacitance of two capacitors connected in parallel
V12: voltage generated when a total charge of 4Q is stored in the capacitors
Thus, it is calculated as shown above
Let us recall the total energy E1+E2 when the two capacitors were isolated from each other.
E1+E2=10/2・Q)2/C
Comparing E12 with E1+E2, the energy E12 is smaller than the isolated energy (E1+E2) by Q)2/C .
In other words, energy is lost when the capacitors are connected. When they are joined into a single unit, the total charge is conserved, yet part of the energy is lost compared with when they were isolated and apart.
Next, we will calculate how the act of connecting them causes this energy loss.
Truth that Contacting of Different Qualities Releases Energy (7)
Vol.13-18
Oct 21, 2025
Content of This Article
Truth that Contacting of Different Qualities Releases Energy (7)
Truth of Bringing Dissimilar Things into Contact – Example 3
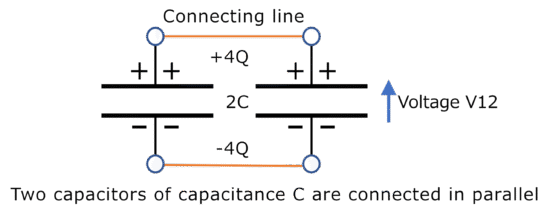
Figure 2-6 Diagram of Capacitors with Capacitance C Connected in Parallel, Each Storing a Charge of 2Q
Let us calculate the energy that is lost. Two capacitors are connected together to form the combined capacitor shown in Fig. 2-6.
There are several ways to connect them. One method is to connect them through a resistor of finite resistance, allowing charge to flow between them. This is illustrated in Fig. 2-7.
When the charge moves, a current flows. We will calculate the current J that flows through the resistor during this process. As time passes, the charge gradually redistributes until it becomes evenly divided between the two capacitors.
The calculation is rather technical, so it is acceptable to skip the detailed derivation here. Below, we first calculate the current J that flows through the resistor R as the charge moves.
J=(V1−V2)/R
Here,
V1−V2: the potential difference between capacitors C1 and C2
During an infinitesimal time interval dt, a small amount of charge dQ moves from capacitor C1 to C2, producing infinitesimal changes d(V1−V2) in the potential difference and dJ in the current.
This relationship can be expressed as:
dV1=−CdQ, dV2=CdQ
Since the infinitesimal amount of charge that moves is equal to the current J multiplied by the infinitesimal time dt,
dQ=Jdt
The infinitesimal change in current dJ can be expressed in terms of the time differential dt as:
dJ=(dV1−dV2)/R=−2dQ/RC=−2Jdt/RC
By continuing to transform the expression,
dJ/dt=J’=-2J/RC
J’/J=-2/RC
㏑J=-2t/RC+Constant
J=exp(-2t/RC+Constant)
When t = 0, J = (3Q − Q)/RC = 2Q/RC, so the constant can be determined, and the expression for the current is obtained:
J=2Q/Rcexp(-2t/RC)
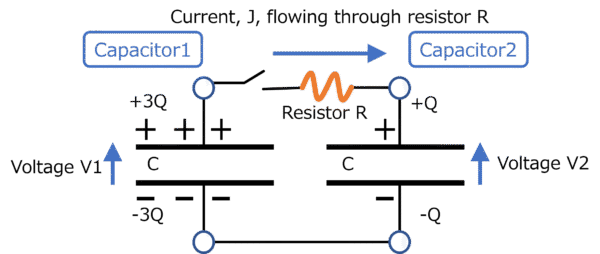
Figure 2-7 Diagram Illustrating the Flow of Charge from Capacitor 1 to Capacitor 2 Through Resistor R
[ Author : Y. F. ]

