次に、可逆的に熱を移動させる可逆熱機関を使って熱を水1から水2に移す方法を考える。そうすると違う答えにたどり着く。
では可逆的に熱をゆっくり静かに移動させることを表現してみる。可逆的ということをエントロピーという熱力学の概念で表現する。
エントロピーの言葉はここでは理解しなくていいが、このあとも登場するので、ここで体験しておく。
可逆的にエネルギーが移動したときには、エントロピーの変化が無い。このエントロピー概念を直感的に分かるように更に付録2を用意した。
それではエントロピーの変化を水1と水2について計算してみる。
水1のそのエントロピー変化をδS1と記述する。水2の変化はδS2と記述する。到達する温度Tmを未知としてTmの温度まで熱を移動させたときのエントロピーの微小変化分を積分する。
付録2より、微小変化分dS=dQ/Tなので
コラムColumn
質の違うものの接触がエネルギーを放出するという真実(3)
Vol.13-18
2025年05月09日
質の違うものの接触がエネルギーを放出するという真実(3)
この記事の内容
質の違うものの接触がエネルギーを放出するという真実(3)
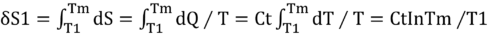
同様に
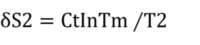
Tmは混ざったあとの仮定した温度である。
仮定した混合温度Tmになるまで水1から水2に可逆熱機関で可逆的に熱移動させる。その後、同じ温度Tmの水1と2を合体(混合)させると温度Tmの混合水ができる。
可逆的であることの表現は全体のエントロピー変化がゼロである(付録2参照)。
全体エントロピー変化の表現はδS1とδS2を加算して得られる。
従って、全体のエントロピー変化
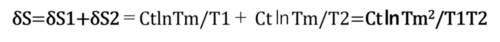
「可逆動作で熱を移動」させることは「全エントロピー変化δS=0」で表現されるので
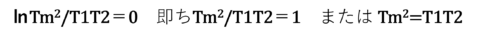
更に表現を変えると
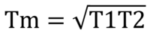
T1=80℃とT2=40℃なら
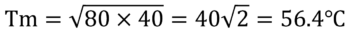
と計算される。
この温度は小学生の答え60℃より低い。温度が下がるのは、外に対して仕事をしたことを仮定したからだ。
この放出してしまう仕事エネルギーを蓄えて、水に戻せば60℃になる。
混ぜるときに仕事エネルギーを外部に放出してしまえば取り戻せない損失エネルギーになる。エネルギー放出なしでは混ざらないという言い方も等価である。
仕事エネルギーを放出して、これを散逸させると、外部からのエネルギーの支援がなければ、元には戻れない。
[ Author : Y. F. ]


